前言
考试 T2 出题人放了个树上斜率优化 DP,直接被同校 OIER 吊起来锤。
离 NOIP 还有不到一周,赶紧学一点。
update:2023.11.14 : 是的第二天我就被吊锤了,发现自己理解的有点问题,所以改一改。

引入
斜率
斜率,数学、几何学名词,是表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
斜率可以用来描述一个坡的倾斜程度,公式\(k = \frac{\Delta y}{\Delta x}\)。
初中学过一元一次函数\(y = kx + b\),这里的\(k\) 就是这个函数表示的直线的斜率。
解决什么
在经典 DP 式:\(f[i] = \min \{ f[j] + val(i,j) \}\) 中,当多项式\(val(i,j)\) 中的每一项仅和\(i,j\) 中的一个有关时,我们可以使用单调队列优化。
但当\(val(i,j)\) 包含\(i,j\) 的乘积项时,就应当使用斜率优化。
然而不同的情况下要使用不同的数据结构来进行斜率优化,如:单调队列(适用于斜率有单调性),二分查找单调栈(适用于x坐标有单调性),平衡树和CDQ分治(适用于x坐标都不单调,实现动态开点和动态插入以及相关维护)
当\(k\) 值和\(x\) 值都单调时用单调队列(这里的单调是指队列中各点的斜率单调,即形成一个凸壳)。
仅当\(k\) 值单调时用单调栈 + 二分查找。因为栈中元素形成的斜率单调,故二分转换时用\(mid\) 与\(mid+1\) 元素的斜率与\(i\) 的斜率作比较来转移\(r , l\) ;(要时刻注意边界,可以通过代入小数据的方法来检查边界)。
理解
下面来以一道题目为例进行讲解。
看完题目应该都可以想出来一个\(O(n^2)\) 的 DP,那就是:
设\(f[i]\) 表示考虑到第\(i\) 个玩具所用的最小花费,\(sum[i]\) 为从\(1\sim i\) 的玩具长度总和。
咱尝试把这一堆东西分分类,把只有\(i\) 的挪到一起,只有\(j\) 的挪到一起,剩下的挪到中间。
得到:
设\(A=sum[i] + i, B = sum[j] - j - L - 1\)。
那么就是 :
显然的,\(A^2\) 咱可以预处理,是已知的,由于前缀和,而且玩具长度至少为\(1\),所以\(2A\) 是严格单调递增的,\(B\) 数组咱也可以直接预处理。
这个式子是把只与\(j\) 有关的移到左边了,可以发现形式上是和\(y = kx + b\) 一样的。
那么咱就可以把一个之前转移完成的状态看成是一个\((B, f[j] + B^2)\) 的点,而\(2A\) 就是经过他们的直线的斜率。
那么咱要求\(f[i]\) 的话,就是求这个点和这个斜率为\(2A\) 的直线的最大可能截距是多少。
于图像中
假设下面的三个点是咱待选的状态:
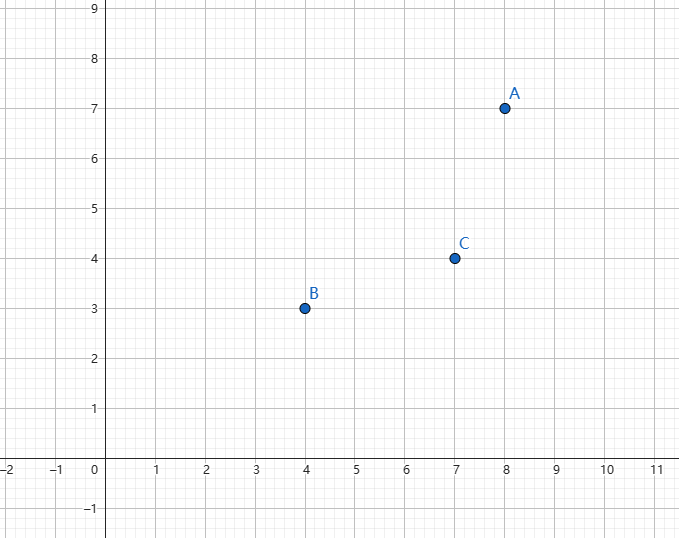
假设咱当前要求的斜率画出来是下面这样:
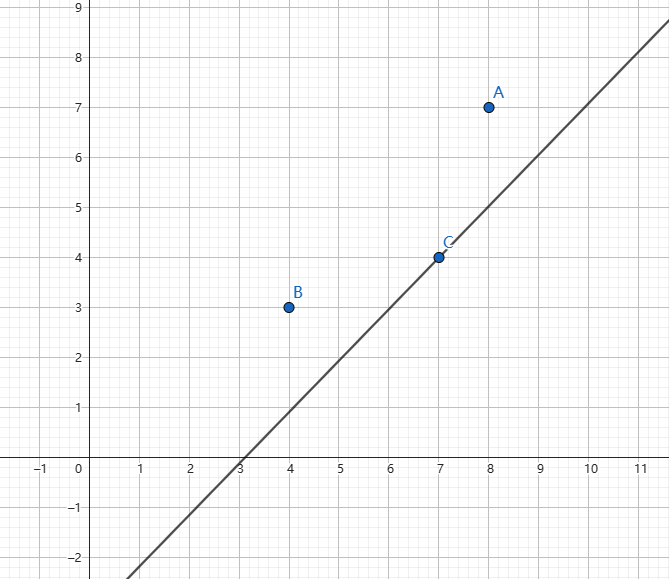
咱就从下往上,一点一点向上挪,直到碰到的第一个点,此时的截距一定最大。咱也能看出的确\(C\) 点最优。
那么此时的\(A\) 点好像没有什么用了,可以扔掉吗?
答案是可以,因为斜率是单调递增的,既然这次第一个碰不到\(A\),那么后面肯定也不是第一个碰到。
但是咱如何做到最快找出呢?
队列维护
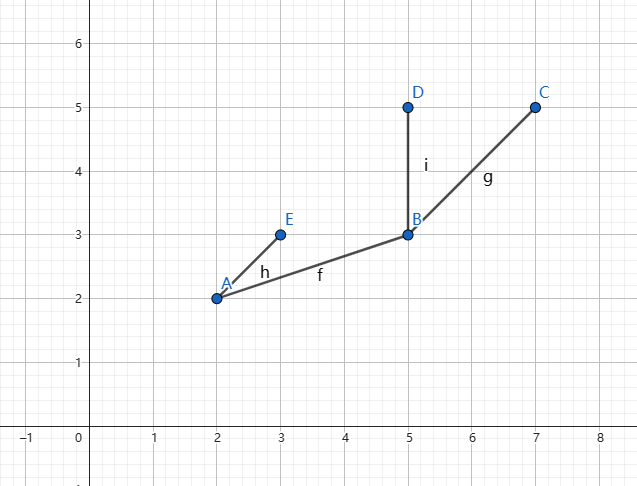
观察这张图片,假设里面的点都是之前转移完的状态。
比较\(AE,AB\) 的斜率。
不难发现\(AB\) 的斜率比\(AE\) 小,想一下之前说的,如果拿一条直线去碰这个图形,从各个角度去碰,最外层的点会形成一个凸包,而这个凸包内的点,是无论如何都碰不到的。
这个咱可以用一个队列来维护一个下凸壳,也就是凸包的一部分。
然后根据上面说的,要是队列头的两个元素形成的直线斜率比当前的小,也可以直接弹出。
这样队列的队头元素就是咱要转移的值了。
code:
/*
* @Author: Aisaka_Taiga
* @Date: 2023-11-13 14:11:27
* @LastEditTime: 2023-11-13 15:09:40
* @LastEditors: Aisaka_Taiga
* @FilePath: \Desktop\P3195.cpp
* The heart is higher than the sky, and life is thinner than paper.
*/
#include <bits/stdc++.h>
#define pf(x) ((x) * (x))
#define int long long
#define DB double
#define N 1000100
using namespace std;
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();}
while(c <= '9' && c >= '0') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * f;
}
int n, L, q[N], c[N], f[N], sum[N], A[N], B[N];
inline int X(int x){return B[x];}
inline int Y(int x){return f[x] + pf(B[x]);}
inline DB xl(int i, int j){return (Y(i) - Y(j)) * 1.0 / (X(i) - X(j));}
signed main()
{
n = read(), L = read();
for(int i = 1; i <= n; i ++) c[i] = read();
for(int i = 1; i <= n; i ++)
{
sum[i] = sum[i - 1] + c[i];
B[i] = sum[i] + i + L + 1;
A[i] = sum[i] + i;
}
B[0] = L + 1;
int h = 1, t = 1;
for(int i = 1; i <= n; i ++)
{
while(h < t && xl(q[h], q[h + 1]) < 2 * A[i]) h ++;
int j = q[h];
f[i] = f[j] + pf(A[i] - B[j]);
while(h < t && xl(q[t - 1], i) < xl(q[t - 1], q[t])) t --;
q[++ t] = i;
}
cout << f[n] << endl;
return 0;
}一般化
咱最后得到的一定是类似这样的方程式:
\(y=kx + b\)
不妨设\(A(x_{1}, y_{1}),B(x_{2},y_2)\) 为两个转移完成的点,假设\(A\) 比\(B\) 优,那么需要满足:
同样的咱可以最后表示成\(f[i] = \dots\) 的形式,然后通过比较两个点的右半表达式最后转化成形如:
这种形式,然后就可以计算是否舍去了。
实现细节
大部分情况下需要将决策点\((x_0,y_0)\) 入队。
保证队列中至少有两个元素(构成直线),单调队列的判断条件要写成\(h<t\)。
建议使用乘积判断斜率大小防止被卡精度,具体参考P5785
最优决策点在上凸包还是下凸包上根据具体方程具体分析。
可能会出现仅满足\(x_i\) 单调不降的情况,此时会造成两直线的斜率相同。可以考虑在求斜率时写成
if (X(x_) == X(y_)) return (Y(y_) > Y(x_) ? 1e18 : -1e18);以及判断决策优劣时写成<=和>=来解决。
例题
咱可以设\(f_{i}\) 表示第\(i\) 个工厂建工厂,只考虑前\(i\) 个工厂不被冲的最小花费。
那么咱就能写出来一个\(O(n^2)\) 的 DP 式子:
复杂度肯定受不了,我们先拆一下式子:
咱设\(s_i = \sum_{k=1}^{i}p_k\times x_k\),然后对\(p\) 数组做一次前缀和。
那么咱就可以简化成这样:
假设前面有两个位置\(a, b\),且\(a<b\) 那么如果\(a\) 转移过来优于\(b\),需要满足:
右边的这个东西可以看作是由\((p_i,f_i+s_i)\) 这类点的两个点构成的直线的斜率,既然\(p_i, x_i\) 单调递增,也就是说斜率需要越来越大,咱就可以维护一个下凸壳。
开一个队列,设\(q_t\) 为队尾元素,那么根据上面的式子,若通过\(q_t,i\) 两个点的直线斜率小于等于通过\(q_{t-1},q_t\) 两点的直线,那么就应该弹出\(q_t\)。
最后有的工厂可能没有商品,所以此时会出现相邻两个点构成的直线中\(p_i-p_j=0\),此时咱想到横坐标相同的两个点,显然应该是要纵坐标更小的。
所以若\(y>0\) 就当作是正无穷,反之则为负无穷,若\(y=0\) 则无所谓。
/*
* @Author: Aisaka_Taiga
* @Date: 2023-11-14 16:17:16
* @LastEditTime: 2023-11-14 19:42:44
* @LastEditors: Aisaka_Taiga
* @FilePath: \Desktop\P2120.cpp
* The heart is higher than the sky, and life is thinner than paper.
*/
#include <bits/stdc++.h>
#define int long long
#define DB double
#define N 1000010
using namespace std;
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();}
while(c <= '9' && c >= '0') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * f;
}
int n, c[N], p[N], x[N], s[N], q[N], f[N], ans = 1e18;
/*
f[i] = min(f[j] + \sum_{k = j + 1}^{i} (x[i] - x[k]) * p[k] + c[i]);
f[i] = min(f[j] + \sum_{k = j + 1}^{i} (x[i] * p[k]) - \sum_{k = j + 1}^{i} x[k] * p[k] + c[i]);
s[i] = \sum_{k = 1}^{i} p[k] * x[k], p[i] = \sum_{k = 1}^{i} p[k];
f[i] = min(f[j] + x[i] * (p[i] - p[j]) - s[i] + s[j] + c[i]);
f[i] = min(f[j] + x[i] * p[i] - x[i] * p[j] - s[i] + s[j] + c[i]);
f[j] = x[i] * p[j] + f[i] - x[i] * p[i] + s[i] - s[j] - c[i];???
*/
inline DB xl(int i, int j)
{
DB y = f[j] - f[i] + s[j] - s[i];
if(p[j] == p[i])
{
if(y == 0) return 0;
else
{
if(y > 0) return 1e19;
else return -1e19;
}
}
else return y / (p[j] - p[i]);
return (f[j] - f[i]) * 1.0 / (p[j] - p[i]);
// return(p[j] == p[i] ? (!y ? 0 : (y > 0 ? 1e19 : -1e19)) : y / DB(p[j] - p[i]));
}
signed main()
{
n = read();
for(int i = 1; i <= n; i ++)
{
x[i] = read(), p[i] = read(), c[i] = read();
s[i] = s[i - 1] + p[i] * x[i];
p[i] += p[i - 1];
}
int h = 1, t = 1;
for(int i = 1; i <= n; i ++)
{
while(h < t && xl(q[h], q[h + 1]) <= x[i]) h ++;
f[i] = f[q[h]] + x[i] * (p[i] - p[q[h]]) - s[i] + s[q[h]] + c[i];
// cout << "CAO : " << q[h] << endl;
while(h < t && xl(q[t - 1], i) <= xl(q[t - 1], q[t])) t --;
q[++ t] = i;
}
h = n; ans = f[n];
while(h && p[h] - p[h - 1] == 0) h --, ans = min(ans, f[h]);
cout << ans << endl;
return 0;
}第一次自己推出来斜率优化。
设\(f_i\) 表示在石头\(i\) 落脚的最小花费。
看到题目咱可以写出一个\(O(n^2)\) 的 DP 式子:
然后咱给他拆一下:
咱设两个决策点\(a,b\) 且\(a < b\),如果\(a\) 优于\(b\),那么要满足:
因为\(h_i\) 严格单调递增,所以咱可以维护一个下凸壳进行斜率优化。
注意青蛙在第一块石头上!
/*
* @Author: Aisaka_Taiga
* @Date: 2023-11-15 17:08:33
* @LastEditTime: 2023-11-15 17:38:43
* @LastEditors: Aisaka_Taiga
* @FilePath: \Desktop\ATDPZ.cpp
* The heart is higher than the sky, and life is thinner than paper.
*/
#include <bits/stdc++.h>
#define pf(x) ((x)*(x))
#define int long long
#define DB double
#define N 200010
using namespace std;
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();}
while(c <= '9' && c >= '0') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * f;
}
int n, m, q[N], f[N], h[N];
/*
f[i] = min(f[j] + (h[i] - h[j])^2 + C);
f[i] = f[j] + h[i]^2 + h[j]^2 - 2 * h[i] * h[j] + C;
*/
inline int X(int x){return h[x];}
inline int Y(int x){return f[x] + pf(h[x]);}
inline DB xl(int i, int j){return (Y(j) - Y(i)) * 1.0 / (X(j) - X(i));}
signed main()
{
int n = read(), m = read();
for(int i = 1; i <= n; i ++) h[i] = read();
int H = 1, t = 1;
q[1] = 1;
for(int i = 2; i <= n; i ++)
{
while(H < t && xl(q[H], q[H + 1]) <= 2 * h[i]) H ++;
f[i] = f[q[H]] + pf(h[i] - h[q[H]]) + m;
while(H < t && xl(q[t], i) <= xl(q[t - 1], q[t])) t --;
q[++ t] = i;
}
cout << f[n] << endl;
return 0;
}咱先对\(x\) 做一次前缀和得到\(A\) 数组,然后设\(S = A[i] - A[j]\)。
那么很容易写出下面的式子:
然后咱设两个点\(x,y\) 且\(y < x\),当\(y\) 更优的时候,必须满足:
由于题目给的\(a\) 是负数,实际上这个斜率是严格单调递减的,所以我们需要维护一个下凸壳。
/*
* @Author: Aisaka_Taiga
* @Date: 2023-11-15 19:34:12
* @LastEditTime: 2023-11-15 19:47:39
* @LastEditors: Aisaka_Taiga
* @FilePath: \Desktop\P3628.cpp
* The heart is higher than the sky, and life is thinner than paper.
*/
#include <bits/stdc++.h>
#define pf(x) ((x) * (x))
#define int long long
#define DB double
#define N 1000100
using namespace std;
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();}
while(c <= '9' && c >= '0') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * f;
}
int n, a, b, c, A[N], f[N], q[N];
/*
S = A[i] - A[j];
f[i] = max(f[j] + a * S * S + b * S + c);
f[i] = f[j] + a * (A[i]^2 + A[j]^2 - 2 * A[i] * A[j]) + b * A[i] - b * A[j] + c;
f[i] = f[j] + a * A[i]^2 + a * A[j]^2 - 2 * a * A[i] * A[j] + b * A[i] - b * A[j] + c
f[x] + a * A[i]^2 + a * A[x]^2 - 2 * a * A[i] * A[x] + b * A[i] - b * A[x] + c < f[y] + a * A[i]^2 + a * A[y]^2 - 2 * a * A[i] * A[y] + b * A[i] - b * A[y] + c
f[x] - f[y] + a * A[x]^2 - b * A[x] - a * A[y]^2 + b * A[y] < 2 * a * A[i] * (A[x] - A[y])
\frac{f[x] + a * A[x]^2 - b * A[x] - (f[y] + a * A[y]^2 - b * A[y])}{A[x] - A[y]} < 2 * a * A[i]
*/
inline int X(int x){return A[x];}
inline int Y(int x){return f[x] + a * pf(A[x]) - b * A[x];}
inline DB xl(int x, int y){return (Y(y) - Y(x)) * 1.0 / (X(y) - X(x));}
signed main()
{
n = read();
a = read(), b = read(), c = read();
for(int i = 1; i <= n; i ++) A[i] = A[i - 1] + read();
int h = 1, t = 1;
for(int i = 1; i <= n; i ++)
{
while(h < t && xl(q[h], q[h + 1]) > 2 * a * A[i]) h ++;
f[i] = f[q[h]] + a * pf(A[i] - A[q[h]]) + b * (A[i] - A[q[h]]) + c;
while(h < t && xl(q[t], i) > xl(q[t - 1], q[t])) t --;
q[++ t] = i;
}
cout << f[n] << endl;
return 0;
}